2025/08/26KAI(カイ)New!
数学解説シリーズ 〜数列『群数列』について〜
こんにちは、進学塾3Arrows高等部小松川CS「KAI」の杉山です。
いよいよ夏も終わりに差しかかっていますが、皆様いかがお過ごしでしょうか。
「めっちゃがんばって成長できた夏だった!!」という人もいれば、
「気がついたら夏が終わりそうで、何もできずに終わったな…」という人もいるかもしれません。
気がついたら時間が経っていて、成長できていないなと感じた人も、そのように感じた今がチャンスです。
過去に戻ってやり直すことはできないので、何事も今開始するのが最速なのです。
この文章を見たことをきっかけに行動を開始してみてはいかがでしょうか。
私の言葉が何かのきっかけになれば幸いです。
さて、前置きはここまでにして、本題に入ります。
以前「mol」について解説したように、多くの人が苦労している内容について解説していこうと思います。
今回は、数列という単元の中で多くの人が苦労する『群数列』について解説いたします。
群数列は、苦戦する人が多いですが、手順通りに解いていけば実はとても理解しやすい分野なのです。
例題
1 / 2,3 / 4,5,6 / 7,8,9,10 / 11,12,13,14,15 / 16,17…
このような群数列があったとき、以下の手順で考えていくと群数列全体の状況がわかり、
小問で何が問われても答えられるようになります。
�@
群で分けなくても数列が成り立つ場合、数列全体の一般項を考える
�A
各群の項数の規則性を考え、第n群の項数を考える
�B
第1群から第n群までの項数の合計を考える
⇒第n群の最後の項が全体で見たときに第何項か
�C
�Bで求めた式のnにn−1を代入する
⇒第n−1群の最後の項が全体で見たときに第何項か
�D
�Cで求めた式に1を加える
⇒第n群の最初の項が全体で見たときに第何項か
�@
1,2,3,4,5,6…なので、一般項はn
�A
第1群には1個、第2群には2個、第3群には3個…となっているので、第n群にはn個
�B
1+2+3+…+n=1/2×n×(1+n)=n(n+1)/2
※
第n群の最後の項が、第n(n+1)/2項ということがわかる
�C
�Bのn(n+1)/2のnにn−1を代入すると (n−1)n/2
※
第n−1群の最後の項が、第(n−1)n/2項ということがわかる
�D
�Cの式に1を加えることで、第n群の最後の項が第(n−1)n/2 +1項ということがわかる。
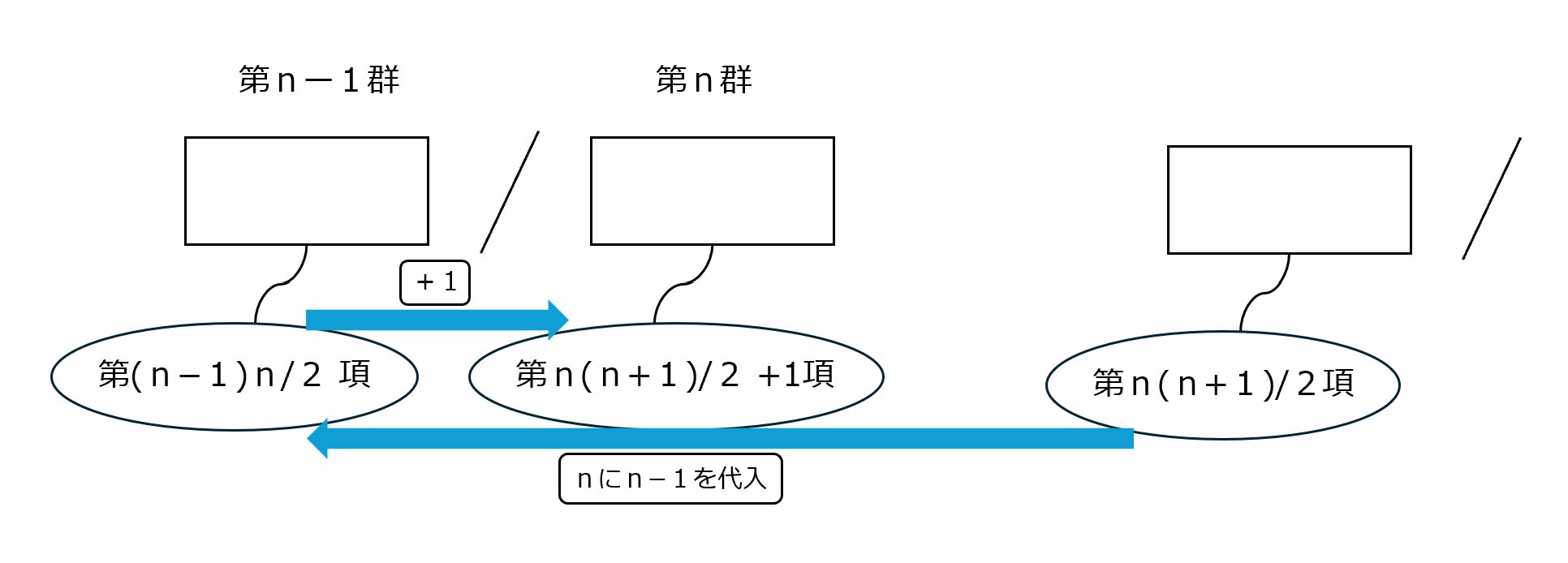
というように、群数列全体の状況を理解しておくことが重要です。
このあと具体的な小問に対してどのように解いていくかは、今回の記事では割愛します。
ちょっと複雑なパターンで説明をしようかと思いましたが、文面だと伝わりにくいと思ったので、群数列としては最もシンプルなパターンで説明しました。
その先の具体的な解き方や、複雑な問題になったらどうすれば良いのかが気になる人はお問い合わせください。
■KAIの自習環境と個別サポート
当塾では、カフェのような落ち着いた空間で集中して勉強できる自習室を完備しています。
また、週に1回チューターの先生との面談を実施し、大学受験に向けて何をすべきか、
どの参考書・問題集に取り組むべきかなど、一人ひとりに合わせた学習アドバイスも行っています。
大学受験は長い道のりです。
一人で悩まず、ぜひKAIの環境とサポート体制をご活用ください。
学習方法や進路選択でお困りの際は、いつでもご相談をお待ちしております。
皆さんの夢の実現に向けて、私たちKAIは常に寄り添い続けます。
3Arrows高等部小松川CS「KAI」は小松川・平井・亀戸・東大島にお住いの
皆様にとって、近隣で通塾しやすく便利で安心です。
成績を上げたい!自分にあった勉強方法を見つけたい!
というやる気のある生徒さんからのご連絡をお待ちしています。
■HP









